17.1.2. Calculation methods
Mathematical explanation of models is described below with a reference to S. A. M. Maleki, H. Hizam and C. Gomes review on "Estimation of Hourly, Daily and Monthly Global Solar Radiation on Inclined Surfaces: Models Re-Visited".
Note: regarding our experience, it is recommended to use Liu Decomposition model and Hay Diffusion model.
Decomposition models:
The global solar radiation on horizontal surfaces can be categorized as follows:
-
Diffuse solar radiation (Ib)
-
Direct beam solar radiation (Id)
Solar radiation on a horizontal surface is the sum of the horizontal direct and diffuse radiation:
Decomposition models typically utilize only data pertaining to global radiation to estimate diffuse radiation from global solar radiation data. Decomposition models are based on a correlation between the diffuse and total radiation on a horizontal surface. It is defined as a function of the hourly clearness index (Mt) and is a measure of the atmospheric effects in an isolated place. Clearness index depends on the time of the year, season, climatic conditions, and geographical situation of a place:
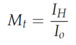 ,
,here and further: Mt -clearness index, IH - horizontal hourly global radiation, Io - hourly extraterrestrial radiation, Id - direct beam solar radiation.
Simple calculation method does not take Clearness index into account and is based on the following expressions:
Kumar's model is used for tropical setting (for example, Madras, India) and is defined by foruth-order polynomial correlation:
Havlader derived a second-order polynomial correlation from data gathered at a tropical site in Singapore:
The same correlation types, data collected from five stations in the U.S. at different latitudes, data range from 1–4 years (considered as a short duration). Hourly values were registered at each of the stations for early normal direct radiation as well as global radiation on a horizontal surface. The difference between these quantities was calculated as diffuse radiation:
Jacovides considered the time interval between 1987 and 1992 in order to measure hourly pyranometric global and diffuse solar irradiation in Athalassa. The data were retrieved from the Cyprus Meteorological Service. The correlations are presented as follows:
Louche used the clearness index Mt to get an estimation on the direct radiation Ib with the following equation:
The correlation provided by Orgill and Hollands is the first of its kind which uses four years of data gathered in Toronto, Canada. Sky cover is categorized into three classes in this correlation, as follows:
A mathematical approach called the Boland-Ridley-Lauret (BRL) model was employed for evaluation based on data gathered in Victoria, Australia. The BRL model comprises a simple exponential correlation:
Diffuse radiation models:
Diffuse radiation models for inclined surfaces. Beam radiation (Ibβ), reflected radiation (Ir), and diffuse radiation (Idβ) are the three components of the global solar radiation incident on an inclined surface (Iβ).
Badescu presented a model for solar diffuse radiation on a sloped surface using the following equation:
Liu and Jordan’s model is one of the earliest and simplest models of radiation. This model presumes that diffuse radiation intensity is distributed uniformly over the whole sky, which is calculated as follows:
Tian proposed the following radiation model:
Another anisotropic model is the one proposed by Hay and Davies, which is commonly referred to as the Hay model. Two primary sources are assumed to be the origins of sky diffuse radiation, namely the disc of the sun disc and the rest of the sky with isotropic diffuse radiation. The two components are described by the anisotropy index fHay:
Based on the Hay model, the equation for the intensity of diffuse radiation on an inclined plane has the form of:
Wilmott adapted the model proposed by Hay and defined a new anisotropy index:
where Cβ = 1.0115 – 0.20293b = 0.080823β2 and β is in radians, and Isc is the solar constant.
The basis of the Perez model is an in-depth applied mathematic analysis of the sky’s diffuse components. This model divides diffuse radiation into three components: isotropic background, circumsolar, and horizon zones. The governing equation is:
In this equation a1 and a2 represent solid angles occupied by the circumsolar region, weighted by its average incidence radiation on an angled and horizontal surface, respectively; F2 and F1, are the dimensionless horizon brightness and the the circumsolar coefficients respectively. The two factors are defined as follows:
These increasing factors set the radiation magnitude values within the two anisotropic regions relevant to those in the major a part of dome. Within the model, the degree of anisotropy could be a performance of solely these two regions. Thus, the model will perform both as an isotropic configuration (F1=F2=1), and collectively incorporating circumsolar and/or horizon brightening equivalent time.
here m is the air mass (dimensionless), Id is the hourly diffuse radiation on a horizontal surface and Io is the extraterrestrial radiation at normal incidence (W/m2). The ε is a function of hourly diffuse radiation Id which is given in table below and direct beam radiation Ib.
The required coefficients Fi,j are obtained from Perez et al., as seen in this table below: